Definiciones básicas

Nudo o nodo: Punto del circuito en el que se conectan 3 o más elementos eléctricos.

Rama: Tramo del circuito que va de un nudo a otro.

Malla: Camino cerrado a lo largo del circuito.

Malla simple: Malla que no contiene ninguna malla en su interior.

 

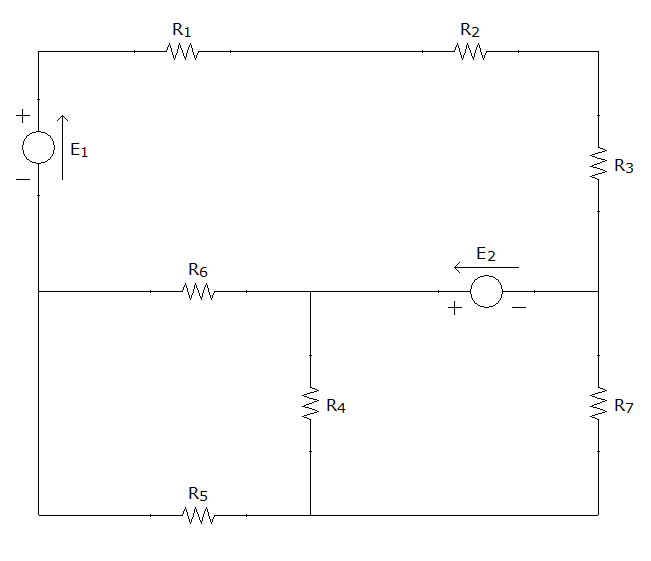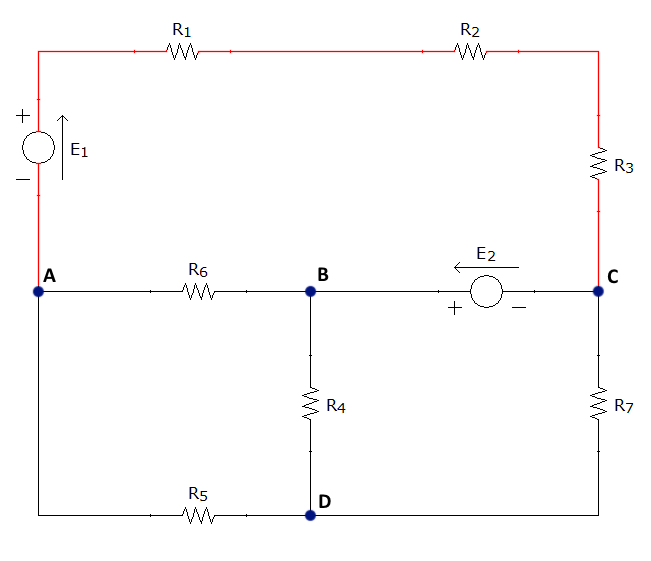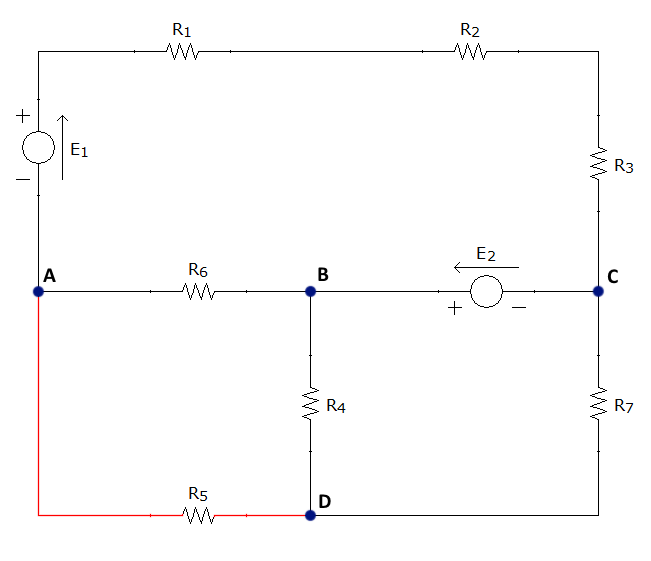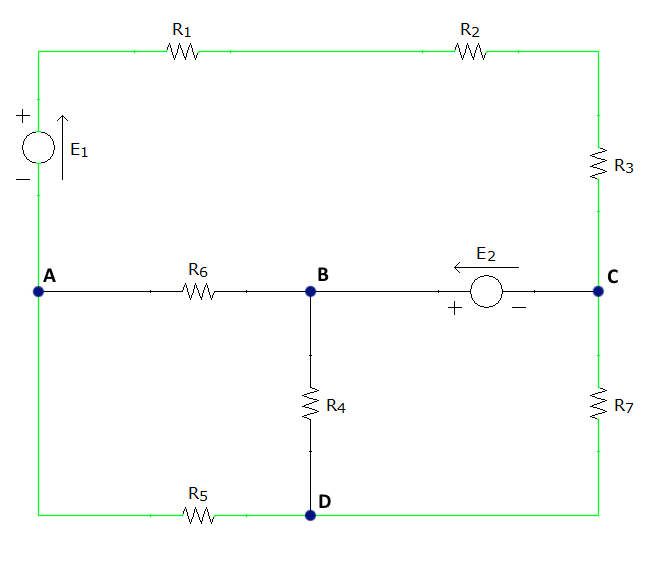
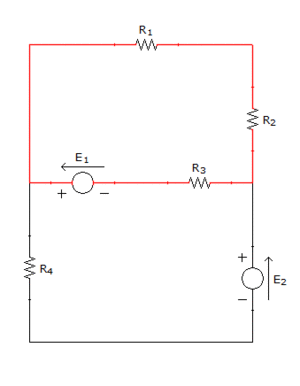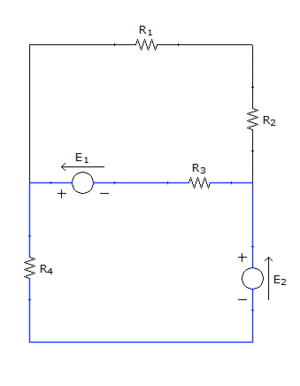
En la siguiente animación se pueden ver en primer lugar los nudos, señalados en azul oscuro, a continuación, las ramas, señalas en rojo, y finalmente, las mallas en verde, siendo las tres primeras simples:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Leyes de Kirchhoff

Primera ley

En todo circuito eléctrico, la suma de las intensidades (o corrientes) que se dirigen a un nudo (que entran en él) es igual a la suma de las intensidades que salen de él.

 

Esto es lo que se ilustra en la siguiente imagen:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Como se ve, en este caso, la intesidad que entra en el nudo es i_1, y las que salen son i_2, i_3 e i_4, por lo que la ecuación de este nudo es:

 

 

 

Segunda ley

A lo largo de todo camino cerrado o malla, la suma de todas las diferencias de potencial (o tensión) es igual a cero. 

 

A continuación se va a resolver un ejemplo práctico para afianzar lo que significa y cómo se aplica esta ley.

 

En primer lugar, se tiene un circuito del que se conocen los valores numéricos de las resistencias y los de las fuentes de voltaje, y lo que quiere obtenerse, es decir, las incógnitas, son las intensidades que circulan por cada rama.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

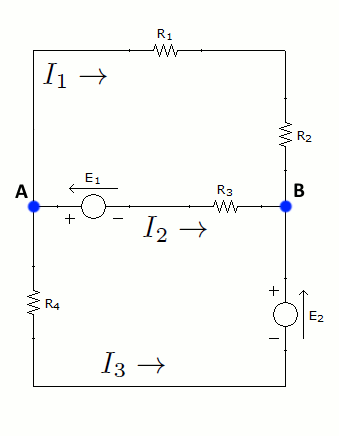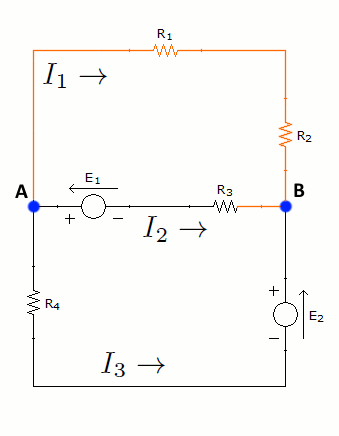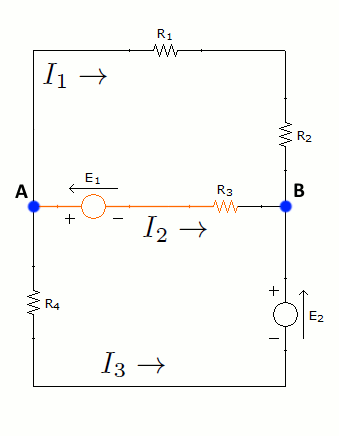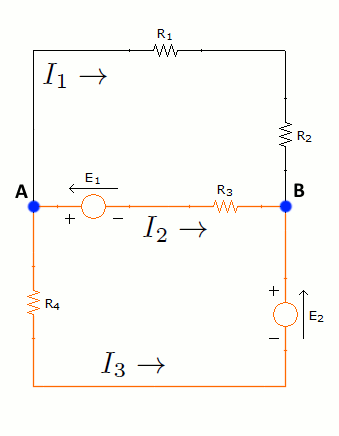
El segundo paso es asignar a cada rama una intesidad (figura de la izquierda). A cada intensidad se le asignará un sentido aleatorio, pues son incógnitas y no se sabe nada de ellas. Al obtener los resultados, si una intesidad es negativa, significará que su sentido real es el opuesto al que se escogió en este paso. Por otro lado, se identificarán las distintas mallas simples, la de color rojo será la malla 1 y la azul la 2 (figura de la derecha):

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

En este paso se obtienen las ecuaciones de las mallas recorriéndolas en sentido horario (también se puede recorrer en sentido antihorario) tal y como se ve en la siguiente animación:

 

 

 

                                                                                                          Ecuación de la malla 1

 

 

 

 

                                                                                                          Ecuación de la malla 2

 

 

 

 

 

 

 

 

 

Aclaraciones:

• Cuando una intensidad atraviesa una resistencia se produce una caída de potencial, por eso el signo de este producto es negativo. 

• Cuando una fuente de voltaje se atraviesa del terminal positivo al negativo se produce una caída de potencial, luego el signo de este valor ha de ser negativo, en el caso contrario, cuando se atraviesa del terminal negativo al positivo, este valor tiene carácter positivo.

• Si la intensidad que recorre la rama en cuestión va en sentido contrario al sentido en que se está recorriendo la malla, dicha intesidad tiene carácter negativo.

• Las caídas de potencial también podrían cosiderarse positivas, es sólo cuestión de criterio, pero hay que seguir el mismo durante todo el proceso para resolver el problema.

 

Aplicación

Este método se aplica de la siguiente manera:

1. Obtener las ecuaciones de todos los nudos menos uno (qué nudo se ignore es indiferente).

2. Obtener las ecuaciones de todas las malla simples.

3. De esta manera se tendrán tantas ecuaciones como incógnitas, y en este paso lo que hay que hacer es resolver el sistema de ecuaciones que se haya construido (en el apartado se anexos se explica el método de Gauss, método muy útil en estos casos).

4. Una vez resuelto el sistema de ecuaciones ya se tienen las intesidades que circulan por cada rama

 

Leyes de Maxwell (o método de mallas)

En el método de Maxwell se le asigna una intesidad a cada malla simple, a esta intensidad se le llama intesidad de malla. Dónde se ha de prestar especial atención es en la ramas compartidas por dos mallas simples.

En el siguiente ejemplo se tienen dos mallas simples, la amarilla y la verde, por las que circulan las intensidades de malla indicadas en la imagen. Cabe preguntarse entonces cuál es la intensidad que circula por la rama que comparten las dos mallas (la rama azul):

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

La intesidad en cuestión es                 , suponiendo que va de izquierda a derecha (     ), o                suponiendo que va de derecha a izquierda (      ).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Con este método de se consigue reducir en el número de incógnitas con respecto al método de Kirchhoff, lo cual hace más sencilla la resolución de los sistemas de los sistemas de ecuaciones resultantes tras la aplicación de este método.

 

A continuación, se obtienen las ecuaciones de las mallas recorriéndolas en sentido horario (también se puede recorrer en sentido antihorario) tal y como se ve en la siguiente animación:

 

 

 

                                                                                                          Ecuación de la malla 1

 

 

 

 

                                                                                                          Ecuación de la malla 2

 

 

 

 

 

 

 

 

 

Aclaraciones:

• Cuando una intensidad atraviesa una resistencia se produce una caída de potencial, por eso el signo de este producto es negativo. 

• Cuando una fuente de voltaje se atraviesa del terminal positivo al negativo se produce una caída de potencial, luego el signo de este valor ha de ser negativo, en el caso contrario, cuando se atraviesa del terminal negativo al positivo, este valor tiene carácter positivo.

• Como se ve, cuando se recorre la malla por la rama compartida entre las dos mallas, la intensidad que se cosidera se obetiene mediante el critero anteriormente mencionado.

• Las caídas de potencial también podrían cosiderarse positivas, es sólo cuestión de criterio, pero hay que seguir el mismo durante todo el proceso para resolver el problema.

 

Aplicación

Este método se aplica de la siguiente manera:

1. Obtener las ecuaciones de todas las malla simples.

2. De esta manera se tendrán tantas ecuaciones como intensidades de malla, y en este paso lo que hay que hacer es resolver el sistema de ecuaciones que se haya construido (en el apartado se anexos se explica el método de Gauss, método muy útil en estos casos).

3. Una vez resuelto el sistema de ecuaciones ya se tienen las intesidades que circulan por cada malla, para obtener las ecuaciones de cada rama hay que restar las dos ecuaciones de malla que circulen por la rama que las dos mallas compartan (en el ejemplo resuelto quedará más claro).

 

Ejemplo comparativo

A continución se ofrece un ejemplo resuelto en el que se comparan ambos métodos:

Descargar ejemplo (El ejemplo aún no está disponible)